
However, such a derivation completely masks the asymptotic behavior of the transform. The implication here is that instead of solving (3.18) for the exact μ n, we have simply approximated it by nπ/( N − 1). In fact, if μ n = nπ/( N − 1) is used in (3.17) then the basis functions in (3.37) are obtained (see Problem 8). It is interesting to note that the eigenvalues in (3.36) and those for the KLT in (3.17) are identical in form. The physical interpretation is that for random signals of very high correlation (ρ → 1), DCT-I, which depends on (3.35) being vanishingly small, loses its decorrelation power, since it will no longer be the transformation that diagonalizes the correlation matrix of the Markov-1 signal. It is noteworthy to point out that as N tends to infinity and ρ tends to one at the same time (3.35) becomes indeterminate, and may not be ignored. (3.37) v n ( m ) = γ n γ m 2 N − 1 cos ( n m π N − 1 ), n, m = 0, 1, …, N − 1.Įquation (3.37) is identical to equation (2.52) in Chapter 2, which defines the elements of DCT-I. The optimal radius of upper plate R and the optimum distance between both plates H were found out by making average value of S minimum. By adding virtual error to the accelerations of ( a, ω) up to 10%, the set of calculated accelerations (a C, ω C) from equation 5 and the average of evaluation value S calculated from equation 6 were obtained. In this time, we calculated normalized radius of upper plate ‘R’ and normalized distance between two plates ‘H’ according the centerline, when bottom plate radius is fixed to 1. And nodes are placed evenly spaced apart (120degrees interval). The centerline, which connects centers of plate, is vertical to both plates. Two plates are in a direction parallel each other. Since we use that platform as not an actuator but a base structure of measuring instrument, we found the optimal structure based on Stewart Platform to reduce the influence of misalignment. The coefficient matrix C should be nonsingular matrix, and the calculation results tend to come under the influence of misalignment and measurement errors of each sensors when the matrix C is near singular point. The rank of a matrix product does not exceed the rank of any individual matrix.
Singular matrix full#
If the system does not have repeated eigenvalues, the mode shape matrix is a full rank matrix. A damping matrix that represents damping at a few isolated degrees of freedom (DoFs) will have a sparse matrix that is not of full rank (known as rank deficient). The stiffness matrix is the same if the system is not allowed to have rigid body motion. Alternatively, the rank is the number of non-zero rows (columns) of the matrix after Gaussian elimination.įor an MDoF structural system, usually the mass matrix is a full rank matrix. For example, the rank of a matrix can be said as the number of independent rows or columns the matrix has (whichever is smaller). In linear algebra, it is possible to show that all these are effectively the same. There are many other ways to describe the rank of a matrix.


For a non-square of m × n, where m > n, full rank means only n columns are independent. Thus, a non-singular matrix is also known as a full rank matrix.
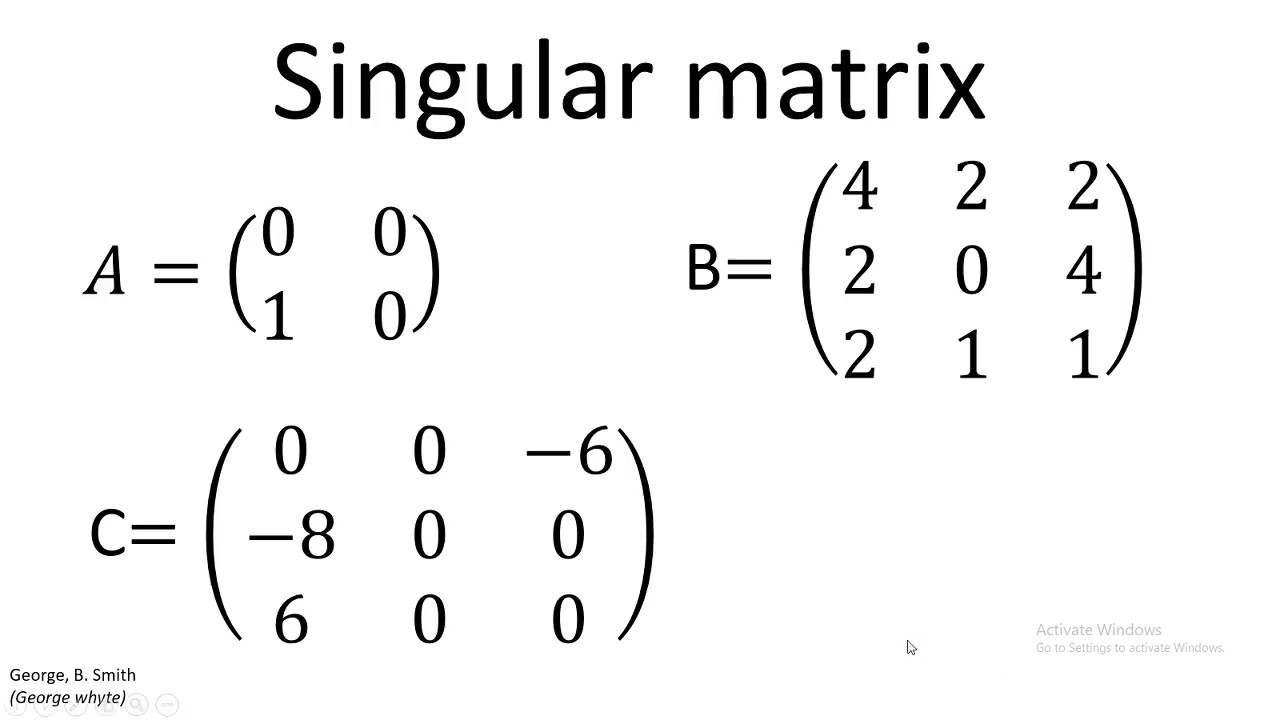
It follows that a non-singular square matrix of n × n has a rank of n. The rank of a matrix is equal to the order of the largest non-singular submatrix of. Jimin He, Zhi-Fang Fu, in Modal Analysis, 2001 2.1.4 The rank of a matrixĪ non-singular matrix is a square one whose determinant is not zero.


 0 kommentar(er)
0 kommentar(er)
